検定

度数曲線の適合度を知るためにKarl Pearsonが検証に用いた方法は、検定と呼ばれる。
これは以下のように導かれる。いま二項分布を考えるとき、大きさnの標本について、理論的な出現率pに対して現実に観測された度数xから、「二項分布」で示したように、その母平均 E(X) と母分散 V(X) は次の式で与えられる。

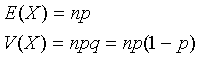
ここで、xを正規分布をする母集団から抜き取られた標本として、その平均と分散をおよびとすれば、次の式で与えられる変量は分布をする。

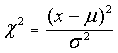
これに二項分布での平均と分散を当てはめることにすると、変量は次のように表せる。

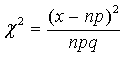
ここで、p+q=1の条件がある上の式を変形すれば、

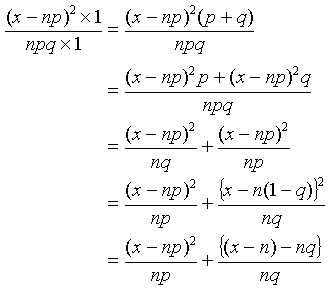
ここで、観測値xを新しい記号Oとし、理論的な出現率npを期待値Eとすることにして、
最初の観測値をO₁、2度目の観測値をO₂、それぞれの期待値をE₁およびE₂と表すことにする。最初の出現確率はpであるから、その出現率はnp、また二度目の出現確率は残る確率qを用いて、nqと表せる。したがって、上の式は、次のように書きなおすことができる。

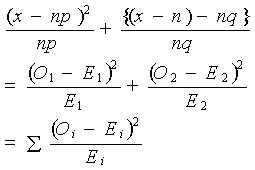
一般的には、互いに排反するk組に分類された値を考え、母集団でのi番目の組に属するし、n個の大標本でのその組の観測値をx_i個として検定に用いる。
多項分布から次式で与えられる変量は、近似的に自由度k-1の分布をする。

出現率p_iは、予め定められた理論値を用いる。もしモデル分布を用いて推定した値を当てはめるならば、自由度をさらに1低くしなければならない。